🏠
🏠
演算処理と数式処理～微分方程式はコンピュータで解こう～
電卓が無かった時代、そろばん名人は実務家としてもてはやされた。ワープロがなかった時代、祐筆は有能な事務方としてもてはやされた。いまだって暗算の名人も書の達人もすごいのだが、電卓とワープロが普及した現在、すごくない庶民だって仕事ができる。
コンピュータが数式を解けなかった時代、微分方程式を解けることはエンジニアの実力のステータスだった。いまだって微分方程式が解ければ、大学院の入学試験で有利であろう。でもコンピュータが数式を解ける現在、庶民だって微分方程式が解ける。
| 概念 | 種類 | 例 | |
|---|---|---|---|
| 数 | 自然数 | 1,2 | |
| 有理数 | -1（整数、負数）,0.5（小数）,1/3（分数） | ||
| 無理数 | √2（無理数）は、根号と数字で表現されます。 π（円周率）、e（ネーピアの底）は数を表現する文字ですが、数字ではありません。 | ||
| 数字 | 算用数字 | 1234567890 | アラビア数字、インド数字と呼び名には歴史的経緯があります。 0という数字の発明により * 、数値に桁（デジット）の概念が導入され、計算が著しく早くなりました。 |
| 漢数字 | 一二三壱弐参 | ||
| ローマ数字 | ⅠⅡⅢⅣⅤ | 11世紀 商人が計算に便利な算用数字を使おうとしていたところ、 ギルドが公文書でその使用を禁止しました * 。 | |
| 数値 | 数量を数字で表現 （デジタル表示） |
3.14,6.02×1023 | 量を数にするには、 単位 が必要です。 ただし、 単位 は、人が決めたものなので、物理の範疇にはありません *。 数値は、数式に代入することができます。 量と量との関係を表現した物理の関係式は、人が決めた 単位 に依存しないので、 単位 を書くべきではありません。 |
数を数字で表現する方法として、アラビア数字による位取り記数法があります。（新 情報技術基礎p.26） コンピュータの内部では、符号付き整数、 倍精度浮動小数点数型（FP64-64bit）、などとして表現されます。
演算 ＝ ある何かと何かを数学的な処理をすること
情報技術基礎, pp.45-46, p.87
MATLAB, Mathematica, Scilab, Sagemath, Octave
Cleve Moler (クリーブ・モラー)
| 型 | 数 | プログラミング言語 | |
|---|---|---|---|
| 整数 | 整数 | Basic (Int), C(int), | |
| 単精度浮動小数点 | 実数 | Basic (Single), C(float), | |
| 倍精度浮動小数点 | 実数 | Basic (Double), C(double), Python (float) | |
| 複素数 | Python (complex) |
測定値などを表す数字のうちで、位取りを示すだけの0を除いた、意味のある数字を有効数字と言う。 たとえば、1.234g±0.012gという測定結果があり、これを 不確かさ を無視して１つの値y=1.234gとして表すことを考える。 不確かさ を考慮した値はおおむね1.222g～1.246gの範囲にあると考えられる。 1 )
このことは、測定値に限ったことではありません。 たとえば、円周率という数には、確かな値がありますが、数字で表現しようすれば、 3.14あるいは3.14159という具合に表現しなければなりません。 やはり有効数字が存在するのです。
さらにこれは10進数に限ったことではありません。 コンピュータの内部では、2進数で表現されることが多くあります。 その表現形式もさまざまです。 単精度浮動小数点や倍精度浮動小数点といった形式があるのは、そのためです 2 ) 。
倍精度浮動小数点は、実数を64ビットで表現します。 実数は無限集合です。それに対して64ビットの表現は264の有限集合です。 実数とデジタル数値を１：１対応させることはできません。 必ず量子化誤差が入ります。
| 項目 | html | MathML | TeX | ASCIIMath | |
|---|---|---|---|---|---|
| 変数 | x | $$x$$ | |||
| 量 | R | $$R$$ | |||
| 量 | Cs | $$C_\mathrm{s}$$ | 量名では、下付き文字は、立体文字（ローマン体）を使います。 MathMLでは、mathvariant属性に"normal"を指定します。 TeXでは、\(C_\mathrm{s}\)とするのに、_\mathrm{s}などと表現します。 | ||
| 化学式 | CO2 | $$\mathrm{CO}_2$$ | |||
| ギリシャ文字 | α,Ω * | $$\Omega,\vartheta$$ * python の matplotlibなどでギリシャ文字を \u03b8や \N{greek small letter theta} のように 別文字列 ** を使います。 |
| 要素 | 数式 | プログラミング言語 | |
|---|---|---|---|
| C | python | ||
| 変数 |
public double x; |
||
| 関数 |
double f(double x); |
||
| 関数と従属変数 |
double f(double x) {
return y;
}
|
||
| 定義域 |
|
C では、VBのselect構文のように switch構文では、定義域を指定することはできません。 結局if構文をネストさせることになります。 |
python
では、switch構文はありませんが、
elif構文でネストさせずに定義域を指定できます。
if x == 0:
print('0')
elif x < 0:
print('負')
elif x > 1:
print('正')
else:
print('発散')
|
| 和 |
for ( i = 1; i < n; i ++ ) {
s += k[i];
}
|
for i in range(1, n): s = s + k[i]* |
|
Phthon (パイソン）は、多様なデータ構造が組み込まれているので、データ処理しやすい言語仕様です。 Anaconda（アナコンダ）や、Google Colaboratoyなどの開発環境があります。 Phthonには、数値計算ライブラリNumPyがあります。 NumPyは、CやふFORTRANで、実装されていて、高速で実行できます。 ほかにも、Matplotlib(グラフ描画ライブラリ） pandas(データ分析ライブラリ） TensorFlow(機械学習ライブラリ） OpenCV（画像処理ライブラリ） など便利なライブラリが多数あります。
Computer algebra, コンピュータを用いて数式を記号的に処理するソフトウェア
Mathmatica, Symbolic Math Toolbox MuPAD for MATLAB, SageMath
Stephen Wolfram(スティーブン・ウルフラム)
たとえば4bitで色を表現するとしたら、24=16通りに表現できます。
A T G C A T G C A T G C A T G Cでも2bitしかなかったら、22=4通りしか表現でません。
A T G C A T G C A T G C A T G Cディジタル化とはそういうことです。
| 項目 | デジタル | アナログ |
|---|---|---|
| 表現 |
20:04
|
|
| 装置例 |
デジタル時計 データロガー ファンクションジェネレータ |
アナログ時計 ペンレコーダ 発振器 |
| 特徴 |
数字（文字）
測定数値を正確に表現 |
量（
角度・長さ）
連続的で微妙な変化を一目で直感的に表現 |
| 精度 | 有限（桁数） | 無限 |
| 時間遅れ※1 | あり | なし |
| 媒体 間のコピー | 容易・高速 | |
| 順序※2 | あり | なし |
| 約束事 | あり | なし |
| 曖昧さ | なし | あり |
| 感覚 | 論理的 | 直感的 |
| 画像 |
|
|
| 音声 |
|
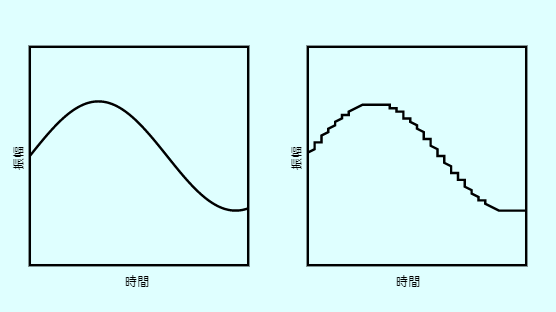
※1. 地上デジタル放送になって、テレビから時報が消えました。 それはデジタル情報には、時間遅れが必ず生じるからです。
※2. デジタルを送るには順序が必要です。エンディアンやバイトオーダーなどと言われます。 シリアライズと同等の概念です。 本質的には言語の線条化と同じ概念です。
ビット深度が低いと色 数が少なくなります。 ヒメシャラの花の 色 は、背景の色と区別がつかなくなります。 解像度（画素数）が低いと矩形（ブロック）になります。 ブロックノイズ は、解像度（画素数）の 量子化ノイズです。 ビット深度が低く、解像度（画素数）が低いほど、情報量も小さくなります。
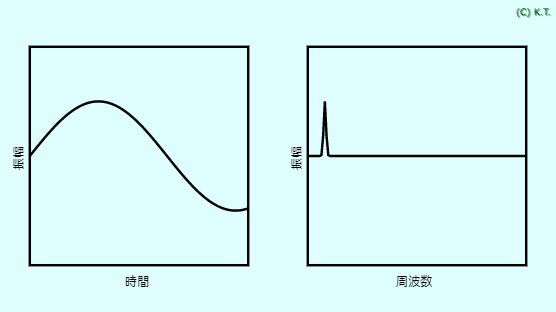
横軸が周波数のグラフを、 スペクトルと言います。 フーリエ変換は、横軸を時間から、周波数に変換する方法です。 デジタルコンピュータの発展で、さまざまな応用ができるようになりました。
時間領域と周波数領域 を変換する フーリエ積分を、離散量に置き換えて近似したものをデジタルフーリエ変換（ＤＦＴ）と言います。 ＤＦＴは行列演算として表現できます。
フーリエ変換というのは、音を聞いて音程を言うようなものです。 音は時間に対する圧力変化です。音程は周波数に対応します。 このように時間の関数を周波数の関数に変える計算方法がフーリエ変換です。 高速フーリエ変換とは、その計算回数を減らしたアルゴリズムです。
協力：ウルフラムリサーチ
微分や導関数，極限値，不定積分，定積分，微分方程式の解法はマセマティカできる時代です．
山形大学大学院理工学研究科の過去問を解いてみよう.
マセマティカは，楽器の演奏もできます．MathematicaのSoundとSoundNote という組み込みシンボルを使います．
Sound[{{SoundNote["E5", {0, 0.75}, "Piano"], SoundNote["C", {0, 0.5}, "Piano"]},
{SoundNote["D5", 0.25, "Piano"], SoundNote["E", {-0.25, 0.25}, "Piano"]},
SoundNote[{"C5", "G"}, 0.5, "Piano"]}]
Mathematicaでディープラーニングを行うことができるようです． AIやディープラーニングについては，第11回の授業で触れる予定です．
ラプラス演算子を使って伝達関数を求めよう．ラプラス演算子を用いると，
コイル = Ls, 抵抗 = R, コンデンサ=1/Cs
と記述できる．
オームの法則をつかって伝達関数を求める．例えば，RC並列回路の伝達関数は，
1/(Cs + 1/R)と表せる．
関連科目は，「数学I 微分方程式とRLC回路」，「数学IV ラプラス変換とラプラス演算子」，「情報エレクトロニクス概論 交流回路」に関連するので，伝達関数やRCL回路の詳細はここでは触れない． RCL回路のシミュレーションは，マセマティカを使いましょう．
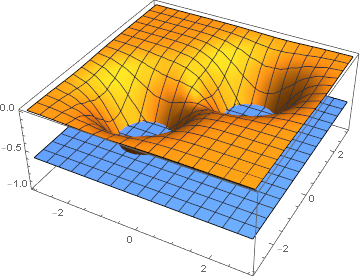
下図はクーロンポテンシャルとＨＯＭＯのイメージです。 クーロンポテンシャルは原子核のまわりにできるへこみみたいなものです。 電子はそこにたまる水みたいなものです。 マセマティカでは、 このような３Ｄイメージを作成できます。
２月１３日からの患者数をシグモイド曲線で最小二乗法でフィッティングして患者数を予測しました。 あくまで現時点のデータ数からの予測なので、予測が大幅にずれることもあります。
Mathematicaには，ウェブベースで使えるOnline版がある． Wolfram Research社は，新型コロナウイルスに対応として，工学部において，Mathematica Onlineが利用できるようになりました． すでに，「Your access to Mathematica | Online Unlimited Site」という件名の招待メールが学生さんに届いると思います． ラインセス管理者からの下記の手順に従ってサインアップして，微分方程式を解いてみよう．大学院入試の過去問は，どうかなぁ．
（１）https://account.wolfram.com/login/oauth2/sign-in にアクセスします
（２）Create One からメールアドレス（ｙｚまたはｓｔ）を登録します
このとき 姓、名、所属等の必要事項を入れます
所属機関: Yamagata University
（３）Wolfram Research から招待メールが届きます
招待メールからアカウントをアクティベートします
（４）https://www.wolframcloud.com/ にログインすればMathematica Onlineが
使用できます
0036 0033 0077 0088
ホームページに公開するとき amenity
