科学技術振興機構.
参考文献の役割と書き方
.
科学技術情報プラットフォーム.
https:/
🏠
🏠
インピーダンスは、周波数の関数です。周波数とともにコールコールプロット（ナイキストプロット）上と ボードプロット上でどのような軌跡を描くか、スライダーをドラッグして周波数を変えてみましょう。
python では、複素数が使えるので、短いプログラムでコールコールプロットのシミュレーションができます。
import numpy as np import matplotlib.pyplot as plt x = [] y = [] R =1000 C = 0.1e-6 for lf in np.arange(0,4,0.1): f = pow(10,lf) w = 2*np.pi*f Z = 1/(1/R+1j*w*C) print(Z) x.append(Z.real) y.append(-Z.imag) plt.scatter(x, y)
インピーダンスは数式１で示されます。
複素平面にプロットしたインピーダンスの周波数による軌跡を コールコールプロットまたは ナイキストプロットと呼びます。
| 直流 | 交流 | |||
|---|---|---|---|---|
| 主な対象 | 界面 | バルク | ||
| 主な評価項目 | 直流抵抗（ ＤＣＲ） | イオン導電率 | ||
| 主な評価方法 | 短絡試験、定負荷試験、定電流試験 | 交流インピーダンス法 、 過渡応答試験 |
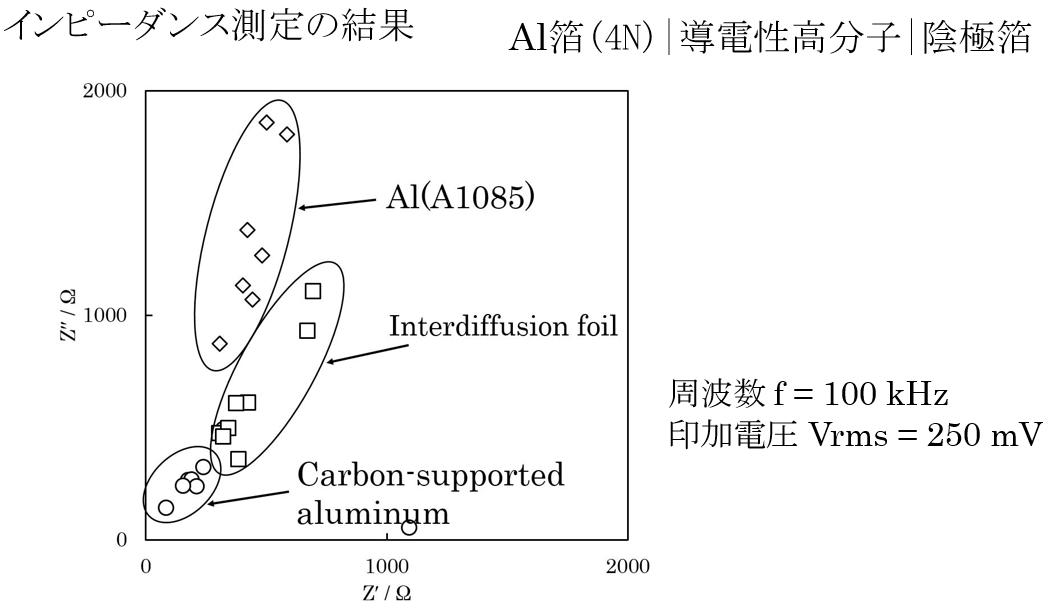
交流インピーダンス法 で測定した、 コールコールプロット の切片は、バルク抵抗（溶液抵抗など）です。 複雑な 電池の内部抵抗 は、 バルク抵抗より界面抵抗に支配されます。 周波数が高いと、界面抵抗と 並列の容量が比較的小さくても（皮膜、 空間電荷層） リアクタンスが小さくなってしまうため、 内部抵抗の推定は、直流抵抗の評価が大切です。
科学技術振興機構.
参考文献の役割と書き方
.
科学技術情報プラットフォーム.
https:/
ろっとん.
RLC直列回路
.
わかりやすい高校物理の部屋.
http:/
佐藤共史.
交流回路の合成インピーダンス
.
電気と資格のお勉強.
http:/
関口理希.
ぼくはメンディ
.
山形大学理工学研究科 修士論文,2018.
https:/
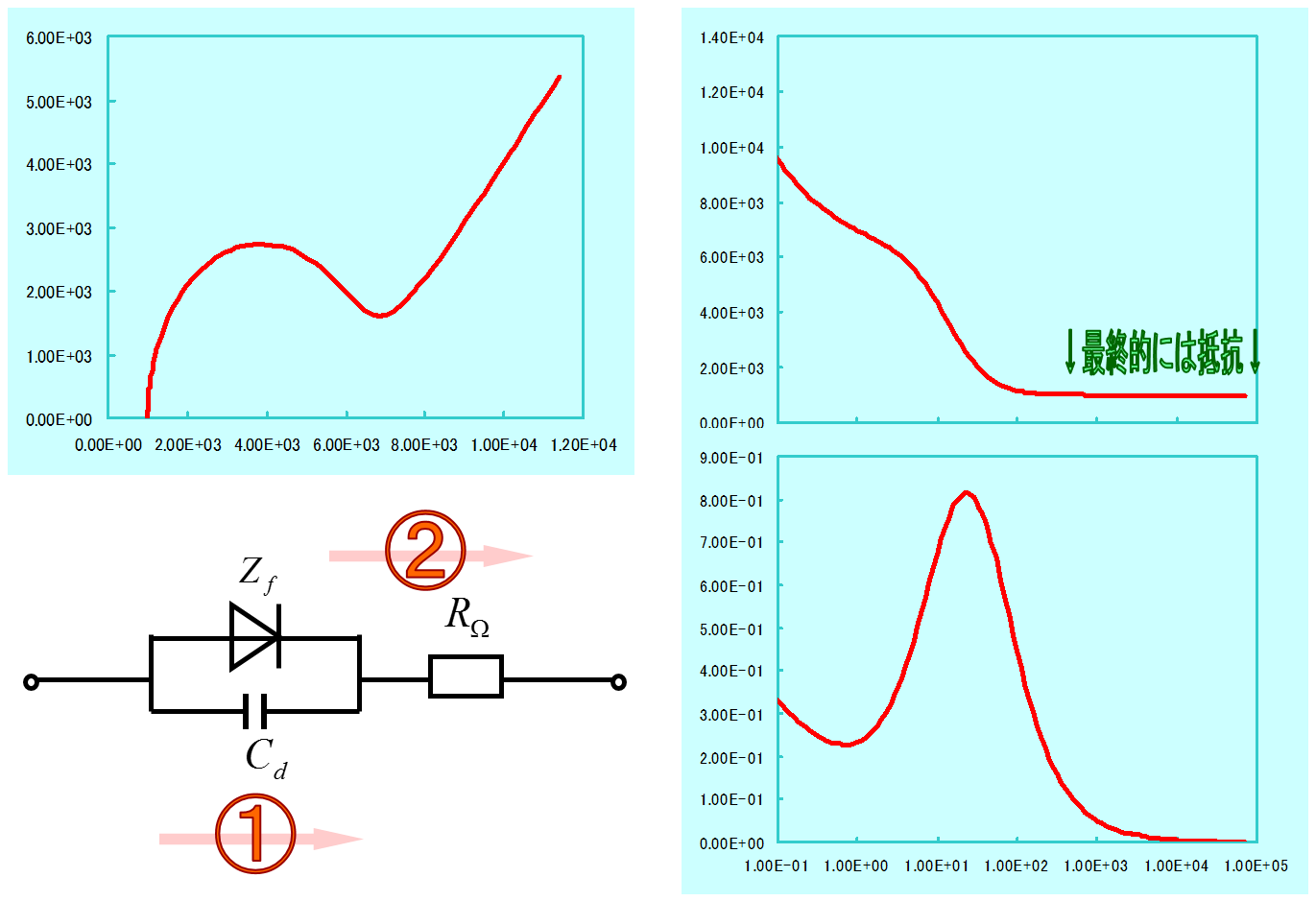
インピーダンスは複素数なので、実部と虚部があります。 実部をリアクタンスと言い、虚部をレジスタンスと言います。 各周波数でのインピーダンスを複素平面上にプロットしたものを コールコールプロットあるいはナイキストプロットと言います。
そもそもなぜインピーダンスを測定したいのか。 等価回路 にフィッティングしたければ、 インピーダンス解析ソフトウェアZView などを使えばいいです。
| 物理量 | 数式 | 備考 | |
|---|---|---|---|
| 周期 T〔s〕 | 🖱山のてっぺんからてっぺんまでの時間です。 | ||
| 周波数 f〔Hz〕 | f = 1/T | 周波数と振幅で交流を表現します。 | |
|
角周波数
|
ω=2πf | ||
| 電圧 振幅Ep0 | 交流の大きさの表現には、振幅のほかにピークトゥピークや実効値があります (※)。 | ||
| 電流 振幅Ip0 | |||
| インピーダンス Z〔Ω〕 | * | ||
| 絶対値 |Z| | |||
|
位相角
|
|||
| アドミタンス Y〔S〕 | * | ||
| インダクタンス L | |||
| 静電容量C | |||
| 電気抵抗 R | インピーダンス Z の実部 | ||
| リアクタンス X | インピーダンス Z の虚部、 X=ωL-1/ωC | ||
| コンダクタンスG | アドミタンス Y の実部 | ||
| サセプタンス B | アドミタンス Y の虚部 |
