🏠
🏠
 🏠
🏠
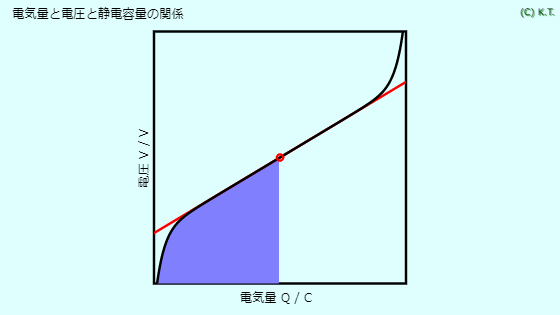
理想的なコンデンサ(キャパシタ)では、電圧は電気量に比例します。
その比例計数が静電容量です。
理想的な電池では、電圧は一定です。なので静電容量は∞です。
実際の電池では、
| 物理量 | 数式 | 備考 | |
|---|---|---|---|
| 周期 T〔s〕 | 🖱山のてっぺんからてっぺんまでの時間です。 | ||
| 周波数 f〔Hz〕 | f = 1/T | 周波数と振幅で交流を表現します。 | |
|
角周波数
|
ω=2πf | ||
| 電圧 振幅Ep0 | 交流の大きさの表現には、振幅のほかにピークトゥピークや実効値があります (※)。 | ||
| 電流 振幅Ip0 | |||
| インピーダンス Z〔Ω〕 | * | ||
| 絶対値 |Z| | |||
|
位相角
|
|||
| アドミタンス Y〔S〕 | * | ||
| インダクタンス L | |||
| 静電容量C | |||
| 電気抵抗 R | インピーダンス Z の実部 | ||
| リアクタンス X | インピーダンス Z の虚部、 X=ωL-1/ωC | ||
| コンダクタンスG | アドミタンス Y の実部 | ||
| サセプタンス B | アドミタンス Y の虚部 |
インピーダンスブリッジや インピーダンスブリッジメーターで 測定します。
電池の性能と言えば、まず電池の起電力、そして内部抵抗。
電池の発熱は、電流の二乗×内部抵抗。 発熱は、無駄な発電負荷であり、無駄な二酸化炭素の排出。 大型電池ほど、放熱が不利になり、熱暴走のリスクが高まります 電池の内部抵抗を下げることが、脱炭素社会への道。
過電圧(電圧降下)=活性化過電圧+濃度過電圧+抵抗過電圧(溶液抵抗+接触抵抗)
インピーダンスと電池の起電力はあまり関係がありません。
インピーダンスで電池の内部抵抗は実部に相当します。
電池の場合、充放電特性と円弧が関係してきます。 でも、1秒間に1万回も電池を充放電することなどないのではないでしょうか? 急速充電といったところで1時間かけて充電ってかんじだとすると、 周波数に直すと1/3600秒で、ミリヘルツの測定になってしまいます。 コールコールプロットの円弧は、そういうところを観察するものなんですね。
交流の電流と電圧の比を インピーダンスと言います。
インピーダンス は複素数なので、実部と虚部があります。 実部をリアクタンスと言い、虚部をレジスタンスと言います 1 ) 。 各周波数での インピーダンスの軌跡を複素平面上にプロットしたものを コールコールプロットあるいはナイキストプロットと言います。
*電池の内部抵抗を小さくするには、電極面積を大きくして、電極間距離を狭めればいいのです。 電極間距離と電極面積の比をセル定数と言います。

平行平板電極であれば、
セル定数a=電極間距離d÷セル断面積S
です。
一般的には、導電率既知のKCl溶液などを使って、セル定数を較正します。
コンダクタンス=導電率
電気抵抗=抵抗率×長さ÷電極面積
| 物理量 | 単位 | 凡例 |
|---|---|---|
| 電極間距離 d | m | 電界の強さ=電圧÷電極間距離 |
| セル断面積 S | m² | 拡面倍率1で、平板モデルのとき電極面積≒セル断面積 |
| 電極面積 A | m² | 実験室でよく使う旗型電極の電極面積は 1cm²。 |
| セル定数 a | 1/m |
セル定数a=電極間距離d÷セル断面積S コンダクタンス G = 導電率 σ ÷セル定数 電気抵抗=抵抗率ρ×セル定数a |
| バルク電流密度j | A/m2 | バルク 電流密度 j = 電流I÷セル断面積 |
| 界面電流密度j | A/m2 | 界面 電流密度 j = 電流I÷電極面積 |
| 電界の強さe | V/m | 電界の強さe = 電圧V÷電極間距離 |
バッテリーはセルを直列につないだストリングを並列につないでいます。ストリングを構成するセルは正極と負極を備えていて、フルセル(全電池)と呼びます。
正極か負極のどちらかひとつの単極の特性を調べるの参照電極(基準電極)を使ってハーフセル(半電池)を構成して測定します。
銀塩化銀電極がポピュラーです。参照電極用銀塩化銀インク(ペーストタイプ)も市販さています。中性水溶液用のほかに有機電解液用、酸性水溶液用、アルカリ水溶液用があります。
液間電位による誤差を減らすには塩橋に飽和KCl水溶液を使うのが効果的です。
界面を表す特性とバルクを表す物性があります。等価回路ではときどき不明瞭なものがありますので、単位で確認しましょう。
界面とバルクの考え方をものにすれば、電気と電池の考え方をだいぶ克服できたようなものです。
たとえばバルクの測定をメインにする導電率測定の導電率計では、 界面インピーダンスを下げるため、電極に300倍もの拡面倍率を持つ白金黒電極を使います。
|
計測可能
な
物理量
(セル) |
界面
の特性値 (面積) |
バルクの
物性値
(セル定数) |
|---|---|---|
|
電気抵抗
R[Ω]
=電圧÷電流
,
|
反応抵抗(面積抵抗率)
Rct〔Ωm-2〕
=電圧÷ 表面 電流密度 接触抵抗 (界面抵抗) * =電圧÷表面電流密度 |
抵抗率(体積抵抗率)ρ
=電場強度e÷ 断面 電流密度 抵抗率ρ〔Ωm〕=電気抵抗R〔Ω〕÷ セル定数 a〔1/m〕 電気抵抗R=抵抗率ρ×長さl/面積S 2 ) 抵抗率ρ=1÷導電率 |
|
コンダクタンスG[S]
=1÷電気抵抗R |
導電率
σ(
|
|
|
静電容量
(キャパシタンス)C
,
|
電気二重層容量Cd〔Fm-2〕 |
誘電率
=電荷密度÷ 電場強度e |
|
インダクタンスL
,
|
透磁率 μ |
電池の内部抵抗は、 バルク抵抗だけでなく、界面抵抗に左右されます。 溶液に金属を浸しただけの ダニエル電池 のような単純な電池では、バルク抵抗が支配的ですが、 合材電極や固体電解質を使う リチウムイオン電池 のような複雑な電池では、界面抵抗が支配的です。 電池の内部抵抗の評価には、 交流評価と直流評価を組み合わせが必要です。
導電率は、電流密度を電界の強さの比です。 電界の強さは電位勾配であり、電位勾配を見るには位置に対して電位を示した電位プロファイルが便利です。
また 導電率は、 移動度 と電荷密度の積です。 移動度は粘度に反比例し、 電荷密度は、イオンの濃度に比例します。
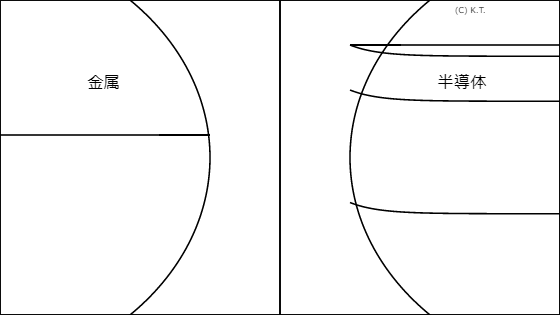
誘電率は、簡単に言えば電荷密度と電場強度金属の比です。
金属は、 金属結合 なので、分極されると、電荷が表面に集まります。このような分極を静電誘導と言います。
活物質は、 イオン結合 なので、分極されると、イオンの位置がずれて電気がたまります。このような分極を誘電分極と言います。

銅 やアルミニウムの金属は、 抵抗率が小さく、 電線や集電体に使われます。
金属は、金属結合しています。 全体に広がった波動関数のエネルギー準位がある導電帯にフェルミ準位があり、電子がバルク全体に非局在化しているからです。

金属酸化物などのイオン結晶は、イオン結合しています。 全体に広がった波動関数のエネルギー準位がある価電子帯にフェルミ準位があり、電子が原子の近傍に局在化しているからです。 電子が局在化して、バルク全体で移動できないという点で、共有結合結晶や分子結晶でも同じです。
グラファイトなどの 炭素材料やポリチオフェンなどの導電性高分子材料では、電子が非局在化できる状態にあり、導電性を示します。
| 界面 | 電位差 | 界面 | 例 |
|---|---|---|---|
| オーミックコンタクト | フェルミ準位が同じになるので、電位差は0 |
(固固界面)
金属|金属 |
銅|アルミニウム |
| 金属|半金属 | アルミニウム|グラファイト | ||
| 金属|半導体 | 白金|酸化チタン | ||
|
(固液界面)
金属| 電解液 |
白金|Fe2+,Fe3+/ aq | ||
| ショットキーコンタクト | 界面電位差 (起電力) |
(固液界面)
金属| 電解液 |
銅|銅イオン水溶液 |
|
(固固界面)
金属|半導体 |
ゲルマニウム|タングステン (接触ダイオード * ) | ||
| 半導体|半導体 | アルミニウム(酸化アルミニウム皮膜)|酸化マンガン(Ⅳ)、 | ||
| 金属| 固体電解質 | 金|ヨウ化銀 |
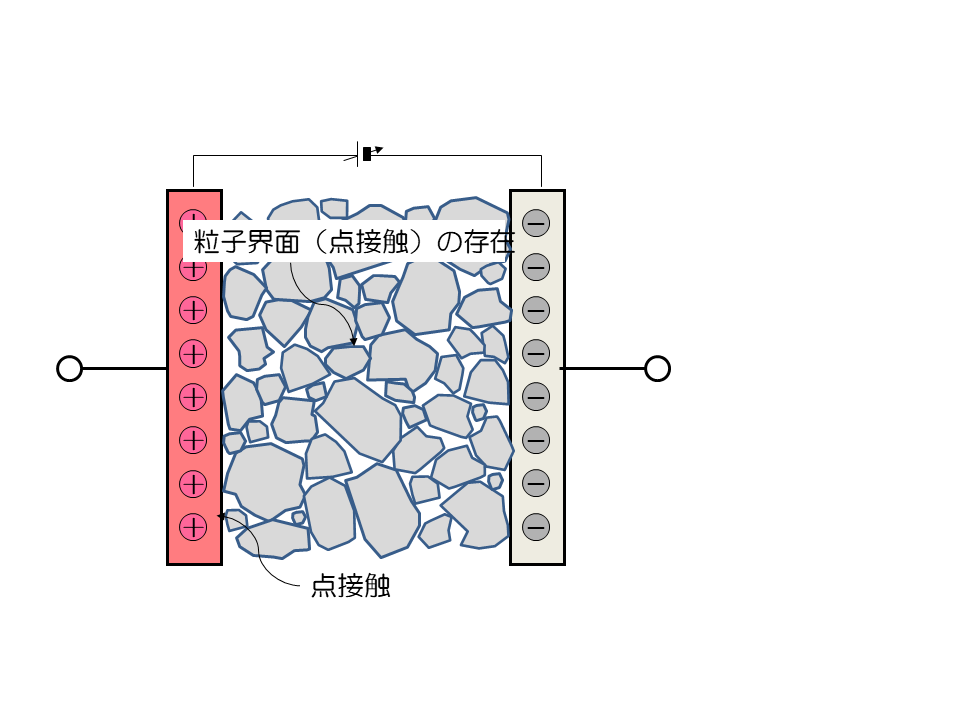
物質と 物質とが 接触すると、その 界面で電気的な相互作用が起こります。
固体同士の接触では、 点接触 になります。 しかし、製膜技術を使ってpn接合などを形成することもできます。
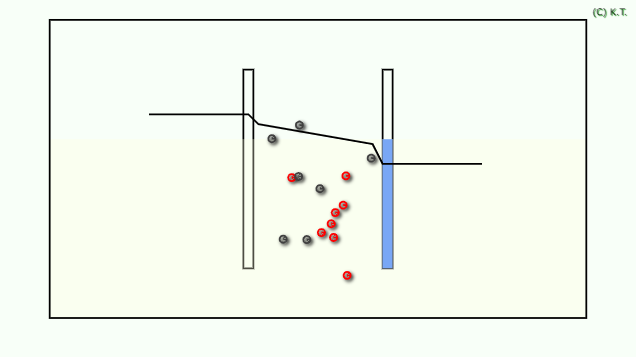
分解電圧を調べるときは、電圧を掃引して、電流を測定します。 これを LSV (リニアスイープボルタンメトリー)ということもあります。 電流電圧曲線から、溶液抵抗の傾きを外挿して、分解電圧を求めます。 理論分解電圧から分解電圧を引いて、 過電圧を求めます。 過電圧を電流密度の対数の関係をターフェルプロットと言います。
電池では、電流を掃引して、電圧を測定します。 求めた電流電圧曲線は、電池の放電の 内部抵抗 を求めるのに使われます。
| 固体 | 液体 | 気体(真空) | |
|---|---|---|---|
| 固体 |
面接触(例:
pn接合) 線接触(三相界面)(例:正極合材、 局部電池) 点接触(三相界面 ショットキー接触 )(例:固体電解質、 炭素導電助剤粒子 ) |
固液界面 (例:サスペンジョン) | 表面 |
| 液体 | 固液界面 (例:電極と電解液) | 液液界面 (例:エマルション) | 気液界面 ( 表面 ) |
| 気体(真空) | 表面 | 気液界面 ( 表面 ) | (混合) |
物質は、 様々な状態をとります。 界面や表面 は、ある材料の相と異なる材料の相が接するところです。
電池の内部抵抗は、バルクと界面との両方から生じます。

空間電荷層を含みます。
Rb+Ri+Rpは、15kΩ以下と推定された。 等価回路
©2020 K.Tachibana