 🏠
🏠
 🏠
🏠
下記の制御スライダーをドラッグして、交流の大きさと周波数を変えてみましょう。

波形の観察、 振幅 や周波数の測定には、 オシロスコープが便利です。 リサージュの観察もできます。
多機能デジタルオシロスコープでは、 ファンクションジェネレータ、マルチメータ、 スペクトルアナライザの機能が搭載されていて、ポテンショスタットさえあれば、インピーダンスの測定も可能です。
⚖️ 電圧直流は、電流の向きと大きさが一定です。 交流は、電流の向きと大きさが時間とともに変化します。
交流はトランスで変圧できるので、エネルギーロスの少ない高圧送電に使われます。
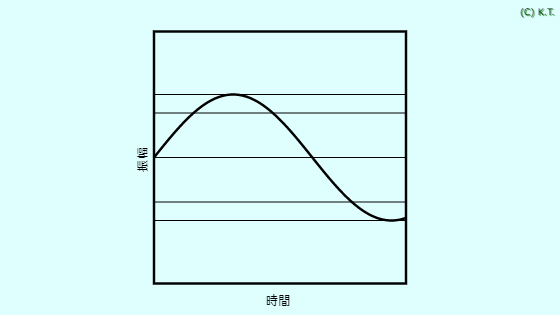
交流は、時間とともに向きと大きさが変わる電気です。
交流の大きさを表すのに、振幅、ピークトゥピーク値、実効値などがあります。
振幅は、この式のE0です。ピークトゥゼロ値などとも呼ばれます。数式で扱うときに便利です。
ピークトゥピーク値は、この式のE0の2倍です。オシロスコープに表示された波形から読み取るときに便利です。Eppなどと書かれたりします。
実効値は、直流で同じエネルギーの電力を送るのと等価な値です。正弦波ではE0の√2分の1です。
繰り返しに要する時間を周期と言います。 正弦波交流の場合、周期は山のてっぺんからてっぺんまでの時間です。 周期の逆数を周波数または振動数と言います。
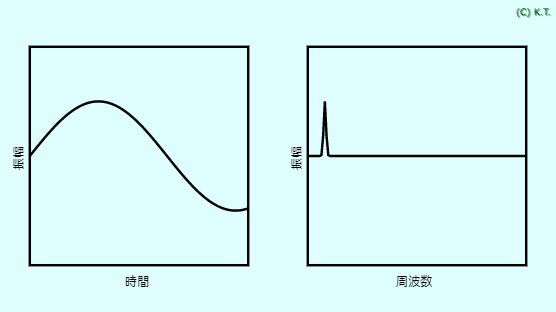
横軸が周波数のグラフを、 スペクトルと言います。 フーリエ変換は、横軸を時間から、周波数に変換する方法です。 デジタルコンピュータの発展で、さまざまな応用ができるようになりました。
正弦波交流の電圧を印加し、印加電圧を横軸、応答電流を縦軸にプロットしたものを リサージュ図形と言います。
インピーダンスにかかわる数式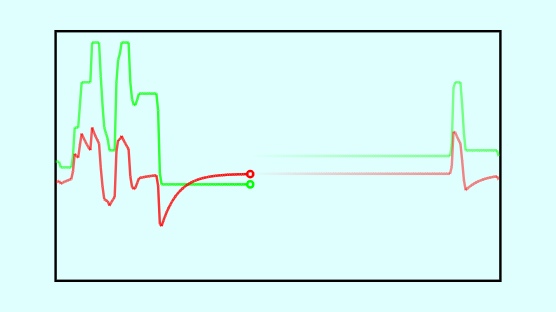
| 物理量 | 数式 | 備考 | |
|---|---|---|---|
| 周期 T〔s〕 | 🖱山のてっぺんからてっぺんまでの時間です。 | ||
| 周波数 f〔Hz〕 | f = 1/T | 周波数と振幅で交流を表現します。 | |
|
角周波数
|
ω=2πf | ||
| 電圧 振幅Ep0 | 交流の大きさの表現には、振幅のほかにピークトゥピークや実効値があります (※)。 | ||
| 電流 振幅Ip0 | |||
| インピーダンス Z〔Ω〕 | * | ||
| 絶対値 |Z| | |||
|
位相角
|
|||
| アドミタンス Y〔S〕 | * | ||
| インダクタンス L | |||
| 静電容量C | |||
| 電気抵抗 R | インピーダンス Z の実部 | ||
| リアクタンス X | インピーダンス Z の虚部、 X=ωL-1/ωC | ||
| コンダクタンスG | アドミタンス Y の実部 | ||
| サセプタンス B | アドミタンス Y の虚部 |
インピーダンスブリッジや インピーダンスブリッジメーターで 測定します。
⚖️ 周波数 ⚖️ 電圧 ⚖️ 電流
インピーダンスが測定できます。
交流 を印加して応答を調べます。
アナログ回路のブロック図