 🏠
🏠
 🏠
🏠
| 種類 | 例 | 説明 |
|---|---|---|
| 文書作成 ワープロ |
|
|
| 表計算 | 数値を計算し、 表 や グラフなどの図表を作成するアプリです。 平均、 標準偏差などの統計量も計算できます。 データ の件数は 30件程度までが適切です。 それ以上の件数の場合、データベースアプリと連携して 抽出した データ を使う方が効率的です。 | |
| 👨🏫 プレゼンテーション |
|
|
| グラフィックス |
|
図形、 地図や 写真などの 画像の作成や編集をします。 |
| CAD | Solid works * | 図面 |
| Autodesk AutoCAD Web | 図面 | |
| 生成AI | Chat GPT Gemini | 文章や 画像の生成をします。 |
| Webページ作成 | HTML editor | |
| データベース | Microsoft Access Microsoft SQL Server | |
| 動画編集 | ||
| 👨🏫 プログラミング |
|
|
| ビジネス ・グループウェア |
|
アプリ には、 オペレーティングシステム (OS) 上で動く、インストールアプリと、 Webブラウザ 上で動く Webアプリがあります 3 ) 。
| 種類 | 分類 | 言語 | 特徴 | |
|---|---|---|---|---|
| インタプリタ | Webアプリ | JavaScript | Webブラウザ上で動作(クライアントサイド) | |
| vb script(vbs,vba,asp) 4 ) | 1964 開発 キーボードとディスプレイが必要 | |||
| AI Webアプリ |
|
matplotlibで、 論文や プレゼンテーションのグラフ作成に。 ビッグデータ データサイエンス * 、 マテリアルズインフォマティクス *、AI | ||
| 教育 | Scratch | ビジュアルプログラミング | ||
| コンパイル | OS | C 6 ) | ポインタ、構造体が扱える。 センサーやアクチュエータを使った 制御。 | 汎用 | VB.NET | オブジェクト指向(多重継承なし) | 汎用 | Kotlin | アンドロイドアプリ向け |
| OS | C++ | オブジェクト指向 |
ファイルベースのシステムでは、コンパイラ言語は実行可能なファイルを生成し、 インタプリタ言語はそれを生成しないという違いがありました。 しかし、クラウドベースになって、実行ファイルそのものをクライアントにダウンロードしなくなり、 ジャストインコンパイルで実行結果だけを利用するようになると コンパイラ言語とインタプリタ言語の違いは、あまり本質的でなくなりました。
科学技術用の伝統的な言語としては、FORTRANがあります。 FORTRAN系列の言語としては、BASIC、pythonがあります。 統計用言語としてRがあります。
アルゴリズム重視の伝統的な言語としてALGOLがあります。 ALGOLは、Pascal, C, C++, C#,java, javascript, typescript, Kotlinと進化してきました。 juliaはCに迫る計算速度を誇ります。
サーバーサイドで使われてきたPerlや Ruby もクラウドで利用できるようになってきました。
人工知能で伝統的な言語Lispは、F#、 Schemeもクラウドで利用できるようになってきました。
人気 プログラミング言語 は、java script、そしてpython*と続きます。 *
| 型 | 数 | プログラミング言語 | |
|---|---|---|---|
| 整数 | 整数 | Basic (Int), C(int), | |
| 単精度浮動小数点 | 実数 | Basic (Single), C(float), | |
| 倍精度浮動小数点 | 実数 | Basic (Double), C(double), Python (float) | |
| 複素数 | Python (complex) |
測定値などを表す数字のうちで、位取りを示すだけの0を除いた、意味のある数字を有効数字と言う。 たとえば、1.234g±0.012gという測定結果があり、これを 不確かさ を無視して1つの値y=1.234gとして表すことを考える。 不確かさ を考慮した値はおおむね1.222g~1.246gの範囲にあると考えられる。 7 )
このことは、測定値に限ったことではありません。 たとえば、円周率という数には、確かな値がありますが、数字で表現しようすれば、 3.14あるいは3.14159という具合に表現しなければなりません。 やはり有効数字が存在するのです。
さらにこれは10進数に限ったことではありません。 コンピュータの内部では、2進数で表現されることが多くあります。 その表現形式もさまざまです。 単精度浮動小数点や倍精度浮動小数点といった形式があるのは、そのためです 8 ) 。
倍精度浮動小数点は、実数を64ビットで表現します。 実数は無限集合です。それに対して64ビットの表現は264の有限集合です。 実数とデジタル数値を1:1対応させることはできません。 必ず量子化誤差が入ります。
| 言語 | 例 | 説明 |
|---|---|---|
| html | <!-- コメント -- > | |
| Python (パイソン) |
# 注釈 """ 複数行にわたる注釈 """ |
#(クロスハッチ)を使います。 """ (トリプルダブルクォーテーション)を使います。 |
| Basic (ベーシック) |
REM 注釈 ' 注釈 |
予約語REMを使うか、'(アポストロフィー)を使います。 |
| C |
/* 1行コメント */ /* 複数行に渡る コメント */ | |
| javascript |
// 1行コメント /* 1行コメント */ /* 複数行に渡る コメント */ |
ほとんどの言語には、注釈機能があります。 人間がよみやすくするためです。 (可読性)
| 言語 | 記述例 | 説明 | ||
|---|---|---|---|---|
| Basic | Dim A As Integer | 整数、浮動小数点、文字列、配列 | ||
| C | 厳密な型宣言 | |||
| Python |
# タプルの配列を円の座標で初期化 t = np.arange(start = 0, stop = 2 * math.pi, step = 0.05) xy = [ (math.sin(p), math.cos(p)) for p in t] |
複素数、リスト、タプル 配列の初期化の記述が柔軟 |
変数には変数名を付けます。 ほとんどの言語では、予約語があり、予約語は変数名に使えません。
変数名の命名規則にはいろいろありますが、スネークキャストがおすすめです。 *
| 言語 | 呼び出し | 説明 | |
|---|---|---|---|
| Basic | Function Sub | 変数のスコープに注意。 | |
| C | 関数名は、関数のポインタの変数とほとんど同義。 | ||
| Python |
#関数定義 再帰呼び出しに挑戦 def func(xy,x1,y1,x2,y2,i): if i < 0: | def ():で宣言。呼び出す前にボディが記述されている必要があります。 関数の記述は、インデントされている必要があります。 |
| 応用例 | |||
|---|---|---|---|
| 無作為抽出 |
extracted = random.sample(data, 10) |
||
| 平均 |
average = statistics.mean(data) average = np.mean(data) |
||
| 標準偏差 |
std = statistics.stdev(data) std = np.std(data) std = np.std(data, ddof=1) # 標本標準偏差 |
||
| 散布図 * |
import numpy as np import matplotlib.pyplot as plt # 乱数を生成 x = np.random.rand(100) y = np.random.rand(100) # 散布図を描画 plt.scatter(x, y) |
||
| ヒストグラム |
import matplotlib.pyplot as plt ax1 = fig.add_subplot(211) ax1.hist(x1, bins=bins) |
||
| 画像 (matplotlib) の例: |
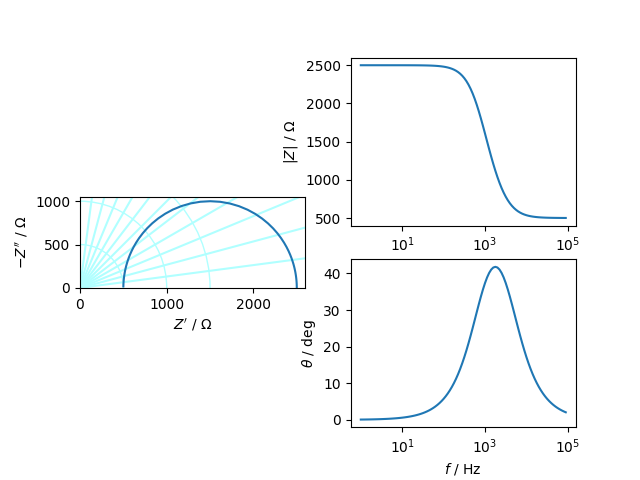
|
Phthon (パイソン)は、多様なデータ構造が組み込まれているので、データ処理しやすい 言語です。 Anaconda(アナコンダ)や、 Google Colaboratoy などの開発環境があります。 Phthonには、数値計算ライブラリNumPyがあります。 NumPyは、CやふFORTRANで、実装されていて、高速で実行できます。 ほかにも、Matplotlib(グラフ描画ライブラリ) pandas(データ分析ライブラリ) TensorFlow(機械学習ライブラリ) OpenCV(画像処理ライブラリ) など便利なライブラリが多数あります。
pymatgenライブラリは、まだあまり普及していない。 *
# ■■■ ★星形 ■■■
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import math
from google.colab import files
xy = [ (math.sin(p), math.cos(p)) for p in \
np.arange(start = 0, stop = 4 * math.pi, step = 4 * math.pi/5)]
fig, ax = plt.subplots(figsize=(5.8, 4.2))
plt.axis("off")
ax.set_aspect('equal');ax.set_xlim([-1,1]);ax.set_ylim([-1,1])
ax.add_patch(patches.Polygon(xy, \
closed=True,facecolor="y",edgecolor="none"))
plt.savefig('star.SVG');files.download("star.SVG")
plt.savefig('star.PNG');files.download("star.PNG")
plt.show()
# ■■■ ★星形 ■■■
# ■■■ ♥ハート形 ■■■
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import math
from google.colab import files
xy = [(math.cos(p), math.sin(p)+math.sqrt(math.fabs(math.cos(p)))) \
for p in np.arange(start = 0, stop = 2 * math.pi, step = 0.02)]
fig, ax = plt.subplots(figsize=(5.8, 4.2))
plt.axis("off")
ax.set_aspect('equal');ax.set_xlim([-1,1]);ax.set_ylim([-1,2])
ax.add_patch(patches.Polygon(xy, \
closed=True,facecolor="r",edgecolor="m"))
plt.savefig('heart.SVG');files.download("heart.SVG")
plt.savefig('heart.PNG');files.download("heart.PNG")
plt.show()
# ■■■ ♥ハート形 ■■■
# ■■■ コッホ曲線 Koch curve ■■■
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import math
import sys
from google.colab import files
sys.setrecursionlimit(100)
#関数定義
def func(xy,p1,p2,i):
if i < 0:
xy.append(p1)
xy.append(p2)
return
else:
x1 = p1[0]; y1 = p1[1]
x2 = p2[0]; y2 = p2[1]
x3 = (x1 * 2 + x2) / 3; y3 = (y1 * 2 + y2) / 3
x4 = (x1 + x2 * 2) / 3; y4 = (y1 + y2 * 2) / 3
xx1 = x4 - x3
yy1 = y4 - y3
xx2 = 0.5*xx1 + math.sqrt(3)/2* yy1
yy2 = -math.sqrt(3)/2*xx1 + 1/2* yy1
x5 = xx2 + x3; y5 = yy2 + y3
xy.append(p1)
func(xy, p1, [x3,y3], i - 1)
func(xy,[x3,y3], [x5, y5], i - 1)
func(xy,[x5,y5], [x4, y4], i - 1)
func(xy,[x4,y4], p2, i - 1)
xy.append(p2)
return
xy = []
n=4
func(xy,[0,0],[1,0],n)
func(xy,[1,0],[0.5,math.sqrt(3)/2],n)
func(xy,[0.5,math.sqrt(3)/2],[0,0],n)
fig, ax = plt.subplots(figsize=(5.8, 4.2))
plt.axis("off")
ax.set_aspect('equal');ax.set_xlim([0,1]);ax.set_ylim([-0.5,1])
ax.add_patch(patches.Polygon(xy, closed=True,facecolor="c",edgecolor="b",lw=0.1))
plt.savefig('Koch.SVG');files.download("Koch.SVG")
plt.savefig('Koch.PNG');files.download("Koch.PNG")
plt.show()
# ■■■ コッホ曲線 Koch curve ■■■
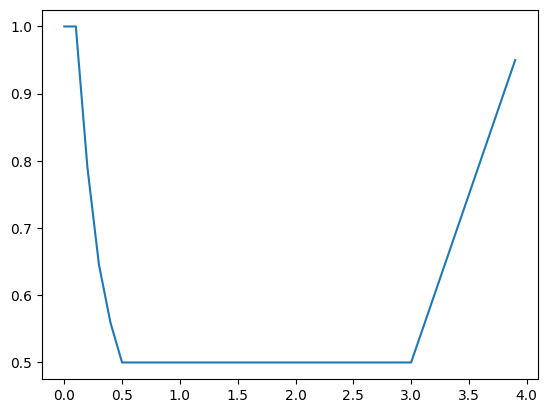
# ■■■ ワイブル分布 ■■■
import math
import numpy as np
import matplotlib.pyplot as plt
alpha = 0.5 # 尺度パラメータ、放射能では半減期、プロセス制御では時定数と呼ばれる
beta = 2 # 形状パラメータ(ワイブル係数)
gamma = 0 # 位置パラメータ
t = np.arange(0, 3, 0.1)
f = [ (beta/alpha)*pow((p-gamma)/alpha,beta-1) * \
math.exp(-pow((p-gamma),beta)/alpha) for p in t]
plt.plot(t, f)
# ■■■ ワイブル分布 ■■■
寿命時間の 確率分布として ワイブル分布が知られています 12 ) 。
散布図を描くには、値域と定義域のそれぞれの集合を準備します。 pythonで、たとえば、0<t<3の定義域のそれぞれの値tiを 設定するには、
t = np.arange(0, 3, 0.1)
とすれば、定義域が0から3、公差0.1の数列が集合として、リスト型の変数に格納できます。
pythonは、このような数学的な概念が、文法として言語に組み込まれているので、 Basic 、 C、 JavaScriptのように forループで繰り返し処理を書く必要がなく、すっきりとしたエレガントなコードを書くことができます。
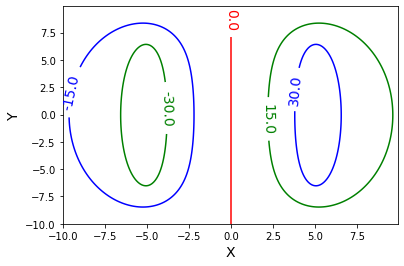
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.1) # x軸
y = np.arange(-10, 10, 0.1) # y軸
X, Y = np.meshgrid(x, y)
Z = 0
for Y_off in np.arange(-7.5,7.5,0.1):
Z = Z + 1/np.sqrt((X-5)**2 + (Y-Y_off)**2+1) - 1/np.sqrt((X+5)**2 + (Y-Y_off)**2+1)
#∞を回避するのに分母に1を足した
cont = plt.contour(X,Y,Z,colors=['r', 'g', 'b'])
cont.clabel(fmt='%1.1f', fontsize=14)
plt.xlabel('X', fontsize=14)
plt.ylabel('Y', fontsize=14)
plt.show()
