圧力と体積

02.エネルギーと生活－動力と電力－

ボイルの法則：圧力と体積は反比例：pV=一定
シャルルの法則：体積は温度に比例：V/T=一定
ボイル・シャルルの法則：pV/T=一定
気体の状態方程式:pV=nRT
pV=m/MRT

熱機関は、 熱エネルギー（温度差）と運動エネルギー（動力）との エネルギー変換 をします。

© 2024 K.Tachibana ^* , C1 Lab.

1824 年S.Carnotが「火の動力に関する考察」を発表しました。 ^{1 )}

👨‍🏫 １９世紀 髙橋

大分類	小分類	特徴用途
液柱式	Ｕ字管マノメーター
	傾斜管マノメーター
弾性式	ブルドン管圧力計
	ベローズ圧力計
	ダイヤフラム圧力計
電気式	抵抗線ひずみ計

圧力 は、物質の 状態や反応速度、化学平衡と関係します ^{2 )} 。 オートメーションで計測されます。

ボイラーでは、高温・高圧の蒸気を作り出します。

温度、 圧力、 流量、 液位 （ 液面）、 組成 （成分、濃度） は、プロセス変量（プロセス変数）と呼ばれます ^{3 )} 。 プロセス変量を計測したり、目標値を設定して、 制御したりします。 PID制御などが使われます。

エネルギー	流体m〔kg〕あたり	流体1kgあたり
運動エネルギー	$\frac{m{\stackrel{\_}{u}}^2}{2}$ 〔J〕	$\frac{{\stackrel{\_}{u}}^2}{2}$ 〔J/kg〕
位置エネルギー	mgZ〔J〕	gZ〔J/kg〕
圧力エネルギー	$\frac{mp}{\mathrm{\rho }}$ $pV$ 〔J〕	$\frac{p}{\mathrm{\rho }}$ 〔J/kg〕

m:質量 $\stackrel{\_}{u}$: 平均流速 $\rho$： 密度

流体を 輸送するには、流体輸送機（ ポンプや送風機）で、配管内を流れる流体にエネルギーを供給します。

👨‍🏫 数式の表現、量の表現

ボイルの法則：圧力と体積は反比例：pV=一定
シャルルの法則：体積は温度に比例：V/T=一定
ボイル・シャルルの法則：pV/T=一定
気体の状態方程式:pV=nRT
pV=m/MRT

熱機関は、 熱エネルギー（温度差）と運動エネルギー（動力）との エネルギー変換 をします。

	🧪 化学	⚡ 電力	💪 動力	🌟 光	🔥 熱
🧪 化学	化学反応	👨‍🏫 🚂 電池 ｐＨセンサー 4 ) 二酸化炭素センサー 湿度センサー	◇ 鉄砲 （ 火薬）	👨‍🏫 化学発光	👨‍🏫 バーナー ◇ 暖炉 ◇ 燃料
⚡電力 eV, FE	◇ 蓄電池 （電解）	変電、 インバータ	👨‍🏫 モーター 5 ) 🔊スピーカー	◇ ＬＥＤ	👨‍🏫 ヒーター 電気炉 Q=I2R
💪動力 pV	◇ 高圧合成	👨‍🏫 発電機 🎤マイク	リンク、カム	◇応力発光	👨‍🏫 ヒートポンプ 🚂 エアコン 6 ) pV=nRT
🌟光 hν	◇ 光合成 銀塩写真	👨‍🏫 太陽電池 イメージセンサー		◇蛍光	👨‍🏫 ◇ 電子レンジ
🔥熱 RT	◇ 加熱合成	👨‍🏫 熱電変換 温度センサー	👨‍🏫 🚂 熱機関 pV=nRT	◇ 白熱電球 （ 黒体放射）

	仕事	熱
エネルギー	エンタルピー	エントロピー
流動	慣性力	粘性力
物質移動	泳動	拡散
固体・ 粉体	慣性力	摩擦力

レイノルズ数

アリはなぜ泳げないか？

^{7 )}

kWh、 J	関係式	示強性変数	示量性変数	物質量あたり マクロ	粒子あたり ミクロ
🧪 化学エネルギーG	⊿G=⊿H-T⊿S	化学ポテンシャル	物質量〔mol〕	アボガドロ数 NA
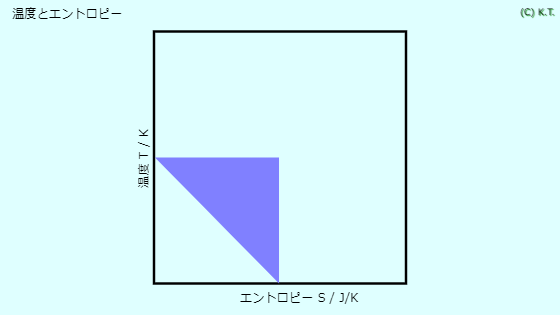
🔥 熱エネルギー	🖱 Q= TS RT	温度 T 〔K〕	エントロピー S 〔J/K〕	気体定数 R 〔J/K・mol〕	ボルツマン定数  kB 〔J/K
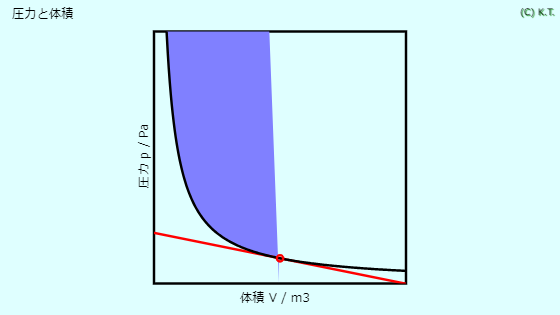
💪 力学的エネルギー  E	🖱 W= pV	圧力 p 〔Pa〕	体積 V 〔m3〕	理想気体のモル体積 x 〔L/mol〕
⚡ 電気エネルギー E	🖱 E=VQ E=nFE	電圧 V 〔V〕	電気量 Q 〔C〕	ファラデー定数 F 〔C/mol〕	電気素量 e 〔C〕
🌟 光エネルギー E	E=hν	振動数 ν 〔Hz〕			プランク定数 h 〔J・s〕

エネルギーは、相互に エネルギー変換できます。 エネルギーは保存則でなくなりませんが、有効な仕事として利用できるエネルギー（エクセルギー）の割合は減っていき、廃熱（アネルギー）の割合が増えていきます。 その意味で、熱エネルギーはエネルギーの廃棄物と言えます。

状態量

物理量 / 単位	説明	応用例
質量 m	天秤で 計測 します。
物質量 n	物質量を直接計測するのは困難なので、 固体や液体は、質量を 計測 し、式量から換算します。 液体や気体は、体積を計測 します。
分率 ni
⚖️ 圧力 p,P	圧力計で 計測 します。
温度 T	温度計で 計測 します。
体積 V	液体は、液位を 計測 します。
熱量 q
比熱容量 CV	$C_V=\frac{\delta q}{dT}={\left(\frac{\partial E}{\partial T}\right)}_V$
エンタルピー H	$H=E+pV$
エネルギー E,U
エントロピー S
⚖️ ギブス自由エネルギー G	$G=H-TS$ $G=G\left(T,p,\mathrm{ni}\right)$

熱力学では、物質と 性質を関連させます。 状態量は、性質の状態の 数量的な表現です。

分類	エネルギー源	応用例
人力	～50W
牛
👨‍🏫 馬	1馬力= 0.746kW	👨‍🏫 鎌倉時代 に戦力に
水車
蒸気機関
ガソリンエンジン	ガソリン 100馬力	🚗 自動車
モーター 1831 モーターを発明。

動力〔W〕とエネルギー〔Wh〕は、絶対に間違わないようにしましょう。

流体輸送に必要な軸動力は、理論動力に摩擦などで消費される動力を加えたものです ^{8 )} 。

西暦年　出来事
水車
室町時代　朝鮮使節が日本の水車の驚く
江戸時代　日本で水車が普及 精米・小麦・蕎麦の製粉
1891 琵琶湖疎水 ペルトン水車で発電
◇ 第一次産業革命 （ 鉄鋼 と 石炭 、 動力 ） ▶ 工業社会（Society 3.0）
1776 ワット蒸気機関（外燃機関）の発明 *
◀ ◇ 第二次産業革命 （ 電気と石油 、 エネルギー ） ▶
1816 スターリングサイクル（外燃機関）
1823 電磁石の発明
1824 カルノーサイクル
1831 電磁誘導の発見
1831 発電機の発明
1831 モーターを発明。
1872 ブレイトンサイクル
1877 オットーサイクル
1897 ディーゼルサイクル

動力の水車は、紀元前2世紀ごろに小アジアで発明されたらしい。 以来、再生可能エネルギーの動力として、あるときは製粉、あるときは揚水と使われてきた。 日本では、急勾配の川が多いため、江戸時代にはかなり普及した。 石炭を使う外燃機関の蒸気機関、石油を使う内燃機関のガソリンエンジンやディーゼルエンジン、 そして電気を使うモーターと動力は変遷した。 しかし、二酸化炭素抑制排出で、化石燃料はもう使えない。 水力がマイクロ水力発電などで注目されているが、日本では水利権などの課題があり、なかなか普及しない。

◇ 参考文献