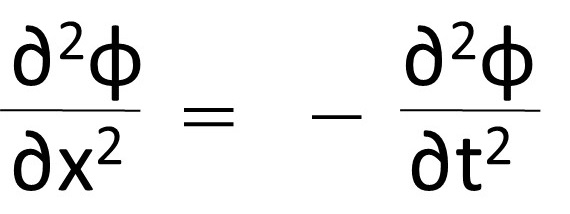
20180628更新
兜山のふもとにある大学に背が高くて握力が60kgある学生がいた。しかも推薦入試で大学に入学しており、さぞ優秀な学生であるに違いない。 しかし学部時代は順位は下から数えた方が都合がよく、GPAも1.8くらいだった。年を召した紳士のような格好をした担任の先生には 「君は3年間GPAが変わらないね」と本当に言われたもんだから、ちょっとくらい頑張った。結果、3年後期のGPAは3前半だったが総計 のGPAは2に届かなかった。そんな学生にとって、波動方程式はその言葉を聞くだけで船を漕ぎ始めるには十分だった。
波動方程式をざっくりと式で表すと下記のようになる(1次元)。
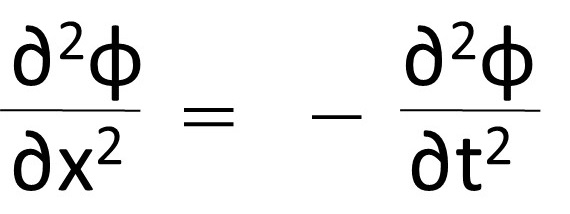
関数φを距離x/mで二階微分したものと時間t/sにマイナスの符号を付けたものが一緒だっていうんだから、 もう頭が痛くなる。こういう時はまず簡単な例で考えてみる。
φ=sin(x-t)
これなら簡単だ!小学生にだってできるぞ!微分!積分!二次関数!
∂φ/∂x = cos(x-t)
∂2φ/∂x2 = −sin(x-t)
距離xで偏微分っつったって、sin(x-t)をxについて微分すりゃいいんだから、そりゃそうだ。次は時間について微分するか!
∂φ/∂x = −cos(x-t)
∂2φ/∂x2 = sin(x-t)
お、役者が出そろったみてーだな!距離で二階微分すると、−sin(x-t)で、時間で二階微分するとsin(x-t)なんだな!ほーぅ・・・ んで、上の頭痛が痛い公式に・・・当てはまるな・・・
つまり、φ=sin(x-t)は解ってことなんだな!すげえ!